Arbitrasjeprisingsteorien (APT)

Alle studiene vi har sett på som dokumenterer at markedet ikke er effisient og at det dermed foreligger alfaverdier forskjellig fra null, har gitt rom for det som kalles arbitrasjehandel.

Å utnytte feilprising av aktiva på en slik måte at en risikofri profitt kan oppnås, kalles arbitrasje. Den meste kjente arbitrasjeprisingsmodellen er APT-modellen.

APT modellen og flerfaktormodeller

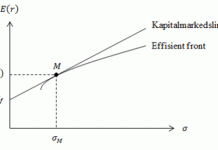
Stephen Ross (1976) utviklet arbitrasjeprisingsteorien (APT). På samme måte som kapitalverdimodellen, predikerer APT-modellen en markedsavkastningslinje som viser sammenheng mellom pris og risiko. Veien de går for å komme frem til denne markedsavkastningslinjen er derimot veldig forskjellig og APT-modellen baserer seg på tre nøkkelforhold (Bodie et al., 2011)

1. Avkastningen på en aksje kan la seg forklare av en faktormodell.
2. Det er tilstrekkelig nok aksjer slik at man kan diversifisere bort usystematisk risiko.
3. Velfungerende aksjemarkeder tillater ikke at det eksisterer arbitrasjemuligheter.

En arbitrasjemulighet oppstår når en investor kan tjene en risikofri profitt uten å foreta en nettoinvestering. Den sistnevnte proposisjonen støttes opp av “loven om en pris” som sier at dersom to aktiva er identiske så vil de også prises likt i markedet.

Loven om en pris tvinges automatisk frem av arbitrasjehandlere som raskt vil utnytte en situasjon hvor to identiske aktiva er priset forskjellig og likevekt vil dermed raskt gjenopprettes. Med bakgrunn i loven om en pris bygger APT-modellen også på færre strenge forutsetninger enn kapitalverdimodellen. En av disse forutsettingene er at investorene er risikoaverse ved valg av portefølje og at de kun er opptatt av gjennomsnittlig avkastning og varians.

I et tilfelle hvor likevektspris brytes forutsetter kapitalverdimodellen, i motsetning til APT-modellen, at et stort antall investorer vil gjøre begrensede endringer i valg av portefølje avhengig av risikoaversjon (Bodie et al., 2011).

I motsetning til i kapitalverdimodellen er det heller ikke noe krav i APT-modellen om at referanseporteføljen i markedsavkastningslinjen er den sanne markedsporteføljen. I APTmodellen er det tilstrekkelig at porteføljen er nok diversifisert til at den usystematiske risikoen blir betydningsløs.

I APT-modellen vil loven om en pris alltid sørge for at to veldiversifiserte porteføljer med lik betaverdi også vil ha den samme forventede avkastningen. Enhver veldiversifisert portefølje liggende på markedsavkastningslinjen vil derfor holde som en referanseportefølje.

En kan for eksempel i APT- modellen definere referanseporteføljen som den veldiversifiserte porteføljen høyest korrelert med en systematisk faktor som en antar har effekt på aksjeavkastningen. En unngår på denne måten problemene assosiert med den uobserverbare markedsporteføljen i kapitalverdimodellen (Bodie et al., 2011).

Hvis vi har to veldiversifiserte porteføljer med lik beta men forskjellig forventet avkastning, vil det være mulig å tjene en risikofriprofitt ved å selge short den porteføljen med lavest forventet avkastning og kjøpe, for tilsvarende beløp som du solgte short, den porteføljen som gir høyest avkastning.

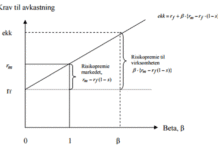
Veldiversifiserte porteføljer med lik beta må derfor ha samme forventede avkastning i likevekt for å unngå at arbitrasjemuligheter oppstår. Veldiversifiserte porteføljer med ulike betaverdier må ha risikopremie som er proporsjonal med verdien på beta for å unngå arbitrasjemuligheter. For å vise dette så tenker vi oss at vi har en risikofri rente på 4 prosent samt to porteføljer hvor portefølje A har en beta lik 1 med forventet avkastning lik 10 prosent, og portefølje B har en beta lik 0,5 med forventet avkastning lik 6 prosent. Hvis vi da lager en tredje portefølje bestående av halvparten investert i portefølje A og halvparten i den risikofrie renten vil denne porteføljen få en beta på 0,5 (0,5×0 + 0,5×1) og en forventet avkastning på 7 prosent (0,5×4 + 0,5×10).

Vi ser da at den nye konstruerte porteføljen får høyere forventet avkastning enn portefølje B, men lik beta, og følgelig vil det oppstå en arbitrasjemulighet som beskrevet i det første tilfellet med like beta.

Vi kan konkludere med at for å unngå arbitrasjemuligheter, må forventet avkastning til alle veldiversifiserte porteføljer ligge på markedsavkastningslinjen, altså den rette linjen fra risikofri rente med stigningstall lik beta. Så vi ser altså at i motsetning til kapitalverdimodellen som krever at referanseporteføljen er den sanne markedsporteføljen, kan APT-modellen bruke en hver veldiversifisert portefølje som ligger på markedsavkastningslinjen som referanseportefølje. Man trenger derfor ikke ta hensyn til problemene som knytter seg til at markedsporteføljen er uobserverbar, og APT-modellen er derfor mer fleksibel. (Bodie et al., 2011). 

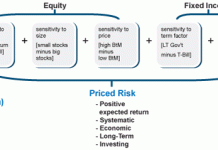
Ved valg av faktorer i modellen er det to viktige prinsipper som gjelder. For det første må vi begrense oss til faktorer som har en betydelig evne til å forklare avkastningen på et aktivum. For det andre vil vi ønske å velge faktorer som fremstår som sannsynlige og viktige risikofaktorer, det vil si faktorer som bekymrer investorer på en slik måte at de vil kreve en meningsfull risikopremie for å utsette seg for slik type risiko.

En alternativ fremgangsmåte ved spesifisering av makroøkonomiske faktorer som kandidater til relevante kilder av systematisk risiko, er karakteristiske egenskaper ved selskaper som på et empirisk grunnlag ser ut til å fungere som referanse for systematisk risiko.

Med andre ord velges faktorene med bakgrunn i variabler som tidligere bevist ser ut til å kunne predikere den gjennomsnittlige avkastning på en god måte og som det derfor er mulig også fanger opp risikopremier (Bodie et al., 2011).