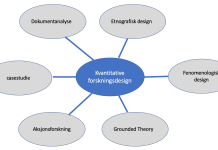
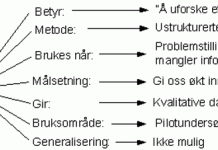
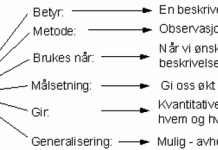
Hva er et eksperimentell design?
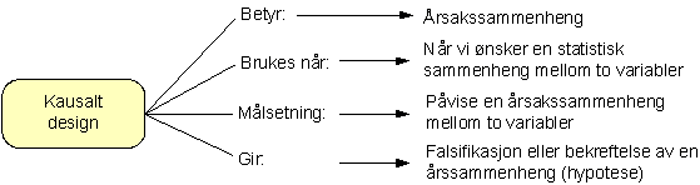
Et eksperimentell design kalles også for et kausalt design. Forskningsdesignet bruker vi når vi ønsker å finne ut om det finnes en statistisk årsakssammenheng (kausalitet) mellom to variabler. Det vil si om om X variabelen er årsaken til Y.
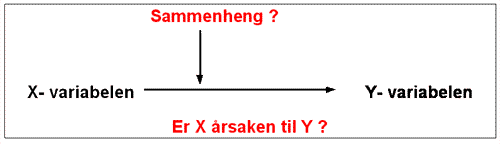
Hensikten med et eksperimentell design er å avdekke hvordan noe påvirker noe annet. Forskeren vil derfor manipulere variabler for å undersøke virkningen av dette. Variabelen vi ønsker å manipulere kaller vi for den uavhengige variabelen, og er den variabelen som vi ønsker å se se virkningen av på en annen variabel. Den variabelen som blir påvirket av den uavhengige variabel kalles for avhengig variabel. Avhengige variabler er de som blir målt for å sjekke effekt.
Bruksområder for eksperimentell design (kausalt design)
Et eksperimentell design (kausalt design) skal gi oss svar på om det er en årsak-virkning forhold mellom to eller flere variabler. Eksperimentell design (kausalt design) er egnet til å løse problemstillinger hvor vi ønsker å måle effekten av et stimulus eller sammenligne effekten av flere stimuli. Målet er å avgjøre om det finnes en årsak-virkning forhold mellom to eller flere variabler.
I markedsforskning og medisinsk forskning er eksperimentell design (kausalt design) mye brukt i forbindelse med effektmålinger.
Alle mellomliggende variabler må utelukkes for å få et gyldig resultat
Et eksperimentell design (kausalt design) blir ofte brukt når vi skal prøve å måle hvordan et markedsføringstiltak påvirker salget. Men det er ikke problemfritt å studere hvordan et stimuli påvirker salget. Det finnes mange problemer som må overvinnes. Sammenhengen mellom stimulus og salg er som regel kompleks og uklar. Dette fordi det er vanskelig å isolere effekten av et enkelt stimulus i en markedsførings-miks. Virkemidlene vil virke sammen og påvirke hverandre. Resultatet at et salg vil være et resultat av mange stimuli og en rekke omstendigheter, ikke ett enkelt stimuli.
Foruten disse interne tiltakene som utgjør markedsførings-miksen vil salgstallene til enhver bedrift bli påvirket av en rekke eksterne forhold i omgivelsene. Forhold som bedriften selv ikke kan kontrollere. Vi tenker da på makro forhold som lokale, nasjonale og internasjonale konjunktursvningninger, lovereguleringer, nye politiske tiltak, lønnsoppgjør o.l. Faren ved disse ikke-kontrollerbare faktorene ligger i at de kan få oss til å trekke feilaktige konklusjoner. Undersøker vi f.eks. om det er en sammenheng mellom en annonsekampanje i Aftenposten og salgsøkningen i en periode hvor konjunkturene blir stadig gunstigere, kan vi komme til å trekke den slutningen at annonsekampanjen har hatt stor betydning for salgsøkningen, mens det i virkeligheten var den generelle optimismen i økonomien som var årsaken til den kraftige salgsøkningen.
Dette problemet kan mer vitenskapelig forklarer slik: Problemet med eksperimentelt design (kausalt design) er at det er vanskelig å slå fast om det er noen sammenheng mellom variablene (annonsekampanjen og salgsøkningen). Selv om det tilsynelatende ser ut til å være en sammenheng mellom X- og Y- variabelen, har det ofte vist seg at det er en mellomliggende variabel (konjunkursvningningene) som er forklaringen til den tilsynelatende årsakssammenhengen.
Dette kan illustreres slik:

I forskningen kan vi derfor aldri bevise med 100% sikkerhet at en variabel (X) er årsaken til effekten (Y). Vi kan bare sannsynliggjøre at X er årsak til Y. Vi kan foreta regresjonsanalyser o.l. for å påvise samvariasjon og beregne konfidensintervall o.l. som gjør at vi med ulik sannsynlighet kan slå fast hvor sannsynlig resultatet er, men vi kan aldri garantere noe med 100% sikkerhet.