Venndiagram

Et venndiagram er en grafisk fremstilling av en eller flere mengder, og eventuelle delmengder. Størrelsen av arealet i diagrammet har ingen matematisk betydning.

Eksempel:

I en klasse på 20 elever har 4 elever spansk og 12 elever fysikk. 2 elever har begge deler. Denne situasjonen kan fremstilles i et Venndiagram:

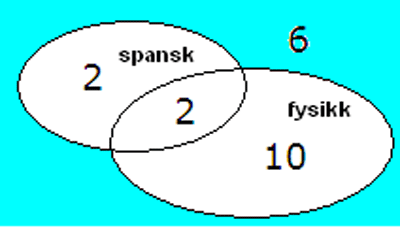
Et venndiagram kan skape klarhet i situasjonen: 6 elever (blå) har ikke spansk eller fysikk. 2 elever har både fysikk og spansk. 4 (2+2) elever har spansk og 12 elever har fysikk. 10 av disse har ikke spansk. Det totale antall elever er 20. En feil som ofte gjøres er at de elementer som er med i flere mengder (spansk og fysikk) telles to (eller flere) ganger.

Krysstabell

Situasjonen med elever i spansk og fysikk kan også presenteres i form av en krysstabell. Da ser det slik ut:

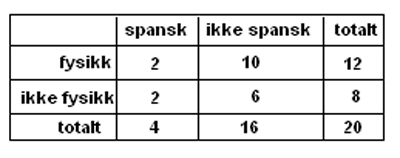
Poenget med begge presentasjonsformer (og med valgtre som kommer lenger nede på siden) er å systematisere ved utvelgelse, slik at det blir lettere å se hva som er gunstig av antall mulige.

Komplementære hendelser

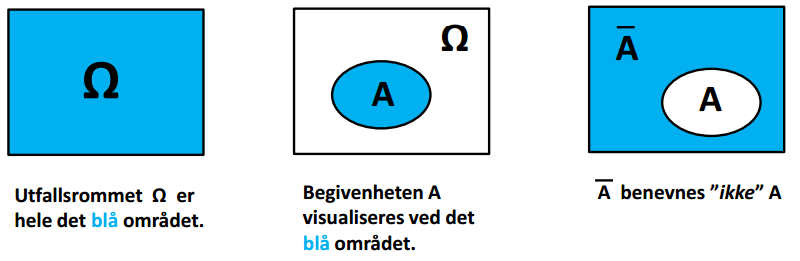
I en klasse har noen elever spansk valgfag. Man skal velge ut en elev fra klassen, og definere hendelse A = ”elev har spansk valgfag”. Alle elever som ikke har spansk valgfag vil inngå i mengden som er komplementær til A.

Situasjonen kan se slik ut presentert i et Venndiagram:

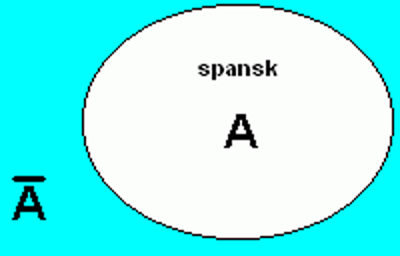
Vi har at P(A)+P(A¯)=1

Union

Union og snitt er begreper som kommer fra mengdelæren. Eksempelvis er A alle som liker matematikk og B er de som liker softis.

Union mellom A og B er da som liker is ELLER de som liker matematikk ELLER de som liker begge deler. 

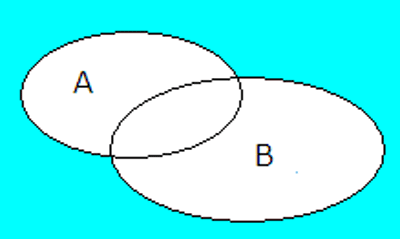
De som liker matematikk eller softis eller begge deler befinner seg i venndiagrammets hvite del, A ∪ B.

Sannsynligheten for å trekke en person som liker softis eller matematikk, eller begge deler blir P(A ∪ B)

Snitt

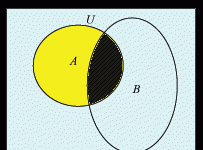
A snitt B er de som liker matematikk OG softis. Symbolet er ∩ og det kan se slik ut i et Venndiagram:

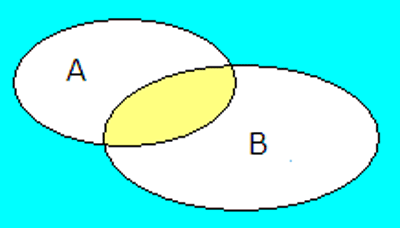
De som liker både matematikk og softis befinner seg i venndiagrammets gule del, A∩BA∩B .
Sannsynligheten for å trekke en person som liker softis og matematikk blir P(A∩B)

Disjunkte hendelser

A og B er disjunkte mengder fordi ingen elementer er felles. Dersom A er personer som liker is og B er personer som liker brus er det i denne mengden ingen personer som liker både brus og is. Det er imidlertid en gruppe (blått) som liker verken is eller brus.

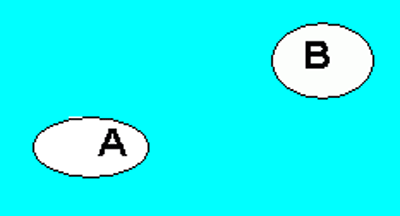
Siden A og B ikke har noen felles elementer skriver vi A ∩ B = Ø. Tegnet Ø betyr den tomme mengde.

Oppsummering

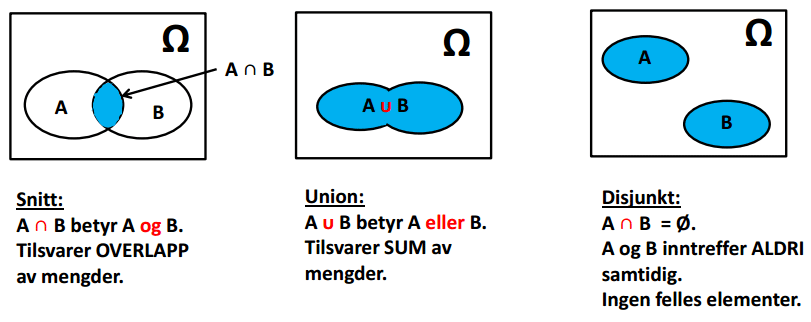
∩ = OVERLAPP av mengder
∪ = SUM av mengder

Kilde:

• http://matematikk.net/side/Sannsynlighet