Hva er en bivariat analyse?
Mens en univariat analyse er en analyse av en variabel, er en bivariat analyse en:
“Analyse av sammenhengen mellom to variabler”
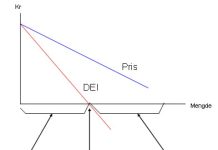
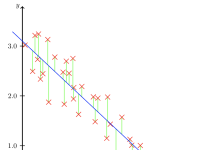
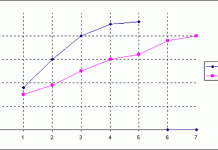
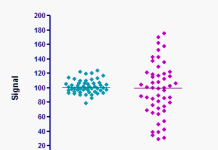
En bivariat analyse, eller todimensjonal analyse på norsk, er en analyse av to variabler og hvordan disse forholder seg til hverandre. Vi ser her på om det finnes en empirisk sammenheng mellom en X og Y variabel. Bivariate analyser benyttes derfor når vi ønsker å se om det er en samvariasjon (korrelasjon) mellom to variabler og når vi ønsker å finne årsakssammenhenger mellom en uavhengig og avhengig variabel. I likhet med en univariat analyse, kan en bivariat analyse være beskrivende eller inferensielle.
En bivariat analyse kan ikke bestemme kausaliteten mellem to variabler. Dette fordi vi ikke vet hvilken variabel som forårsaker e endring på den andre. Vi kan heller ikke utelukke at det er en tredje mellomliggende variabel som påvirker den observerte sammenhengen mellom to variabler.
For å kunne analysere sammenhengen mellom to variabler må vi koble sammen to frekvensfordelinger ved å krysstabulere dem. Vi får da en helt ny tabell vi kan analysere videre for å finne ut hvordan variablene står i forhold til hverandre. Vi er her interessert i å finne samvariasjon.