Skjevhet og normalfordeling

Hva er skjevhet og normalfordeling?

Når utvalget skal beskrives, vil det alltid være interessant å vite om det finnes skjevheter i utvalget eller om utvalget er normalfordelt. Spesielt viktig er dette hvis vi ønsker å generalisere resultatene til å gjelde hele populasjonen.

For å kunne utføre statistiske beregninger som baserer seg på en normalfordeling, må det ikke være store skjevheter i stikkprøven for at resultatet skal være pålitelig og gyldig. Vis derfor hvordan stikkprøven er sammensatt, slik at leserne av analysen kan danne seg et bilde av hvilke skjevheter som eventuelt finnes i stikkprøven.

For å kunne bruke en normalfordeling må utvalget helst være symetrisk fordelt. Det vil si at avstanden mellom og  skal være lik avstanden mellom og .

Sentralgrenseteoremet – normalfordelt

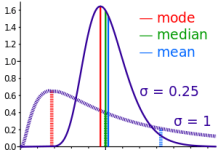
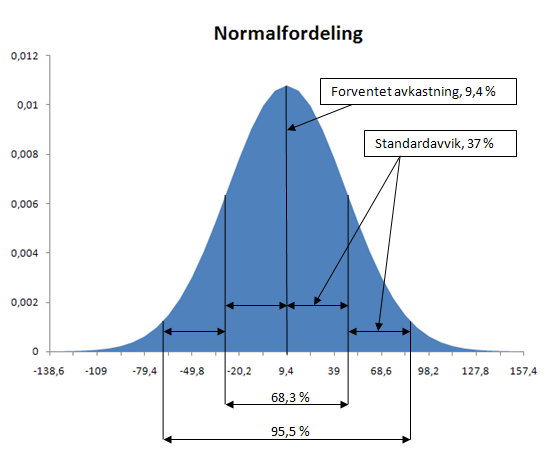
Er utvalget symetrisk fordelt, sier vi at utvalget er normaltfordelt. Normalfordelings begrepet bygger på en teori som kalles sentralgrenseteoremet. En teori som står sentralt i alle undersøkelser som tilstreber statistisk inferens. Det vil si i undersøkelser hvor vi ønsker å kunne generalisere resultatene.

Egenskaper ved normalfordelingen:

1. Symmetri: Normalfordelingen er symmetrisk rundt gjennomsnittet (mean). Dette betyr at høyre og venstre side av fordelingen er speilbilder av hverandre.

2. Gjentakende mønster: Fordelingen er klokkeformet, med de fleste verdiene samlet rundt gjennomsnittet. Verdier langt fra gjennomsnittet er sjeldne.

3. Gjennomsnitt, median og modus: I en perfekt normalfordeling er gjennomsnittet (mean), medianen, og modus (den hyppigste verdien) alle like og ligger i midten av fordelingen.

4. Standardavvik: Områdene under kurven representerer sannsynligheter. For en normalfordeling ligger:

   • Cirka 68 % av dataene innenfor én standardavvik fra gjennomsnittet.
   • Cirka 95 % av dataene innenfor to standardavvik fra gjennomsnittet.
   • Cirka 99,7 % av dataene innenfor tre standardavvik fra gjennomsnittet.

5. Asymptotisk: Halen på kurven nærmer seg, men treffer aldri, x-aksen. Dette betyr at det er en liten sannsynlighet for svært ekstreme verdier, men de er uendelig sjeldne.

Andre viktige karakteristika ved en normalfordeling er:

• Symetrisk fordelt kurve med kun ett “MODE”
• 90% av alle observasjoner ligger i området: Gjennomsnitt +/- 1,64 standardavvik
• 95% av alle observasjoner ligger i området: Gjennomsnitt +/- 1,96 standardavvik
• Nesten alle observasjonene dekkes hvis vi tar tre standardavvik på hver side av gjennomsnittet.

Formel for normalfordelingen:

Den generelle formen for normalfordelingen er gitt ved dens sannsynlighetstetthetsfunksjon (PDF):

For at vi skal kunne bruke teorien om normalfordeling må n>30.

Standard normal distribusjon

Enhver normalfordeling kan transformeres til det vi kaller en “standard normaldistribusjon“. Standard normaldistribusjon har de samme egenskapene som normaldistribusjonen, men midtpunktet er alltid null og standardavviket er alltid lik 1.

Formelen for å transformere en verdi X fra en normalfordeling til dets ekvivalente verdi Z for en standard normaldistribusjon er:

Tegnforklaring:

X   = Variablens verdi

= Gjennomsnittet til variablen i populasjonen

= Standardavviket til variablen

Bruk av normalfordeling:

Normalfordelingen brukes i mange statistiske metoder, inkludert:

• Hypotesetesting: Mange statistiske tester, som t-tester, antar normalfordeling av data.
• Konfidensintervaller: Normalfordelingen brukes til å beregne konfidensintervaller for gjennomsnitt.
• Regresjonsanalyse: I lineær regresjon antar man ofte at restleddet (feilen) er normalfordelt.

Normalfordelingen er en av de mest brukte og studerte fordelinger i statistikk, og dens egenskaper gjør den til et kraftig verktøy i dataanalyse og forskningsarbeid.

Skjevhet

Skjevhet er et mål for usymmetri. 

Skjevhet viser til graden av asymmetri i en sannsynlighetsfordeling av en tilfeldig variabel. Det er en statistisk mål som beskriver hvordan fordelingen av data avviker fra en normalfordeling.

Typer av skjevhet:

Det finnes to hovedtyper av skjevhet:

1. Positiv skjevhet (høyreskjevhet): Fordelingen har en hale som strekker seg mot høyre side, mot de høyere verdiene. I en positivt skjev fordeling er gjennomsnittet ofte høyere enn medianen, fordi noen få høye verdier trekker gjennomsnittet opp. Et eksempel på en positivt skjev fordeling kan være inntektsfordelingen i et samfunn, hvor de fleste tjener moderate summer, men noen få personer tjener svært høye summer.
2. Negativ skjevhet (venstreskjevhet): Fordelingen har en hale som strekker seg mot venstre side, mot de lavere verdiene. I en negativt skjev fordeling er gjennomsnittet ofte lavere enn medianen, fordi noen få lave verdier trekker gjennomsnittet ned. Et eksempel på en negativt skjev fordeling kan være eksamensresultater i et tilfelle der de fleste scorer høyt, men noen få scorer veldig lavt.

De fleste utvalg vil være enten være høyre- eller venstre skjevt. Det som varierer er graden av skjevhet. Utvalgsskjevheter best illustreres i et plott.

Høyreskjev fordeling (postiv skjevhet)

Symetrisk fordeling (negativ skjevhet

Venstreskjev fordeling

Formel for skjevhet

Skjevheten i et utvalg regnes ut med følgende formel:

Mål på skjevhet:

Skjevhet kan kvantifiseres ved hjelp av en skjevhetskoeffisient (ofte kalt Pearson’s skewness coefficient). Denne koeffisienten kan tolkes som følger:

• Skjevhet = 0: Fordelingen er symmetrisk, som en normalfordeling.
• Skjevhet > 0: Fordelingen er positivt skjev (hale mot høyre).
• Skjevhet < 0: Fordelingen er negativt skjev (hale mot venstre).

Betydning av skjevhet:

• Positiv skjevhet: Hvis en fordeling er positivt skjev, kan det tyde på at det er noen ekstreme positive verdier som påvirker datasettet. Dette kan være viktig i økonomisk analyse, der inntektsfordeling ofte er positivt skjev.

• Negativ skjevhet: Negativ skjevhet kan indikere at det er noen ekstreme lave verdier som påvirker datasettet. Dette kan være relevant i vurdering av risiko, hvor uventede store tap (som ved forsikring eller finansielle tap) kan dominere resultatene.

Håndtering av skjevhet:

I statistisk analyse kan skjevhet skape utfordringer, spesielt i metoder som forutsetter normalfordeling (som regresjonsanalyse). Noen vanlige metoder for å håndtere skjevhet inkluderer:

• Logaritmisk transformasjon: Å bruke logaritmen av dataene kan redusere skjevhet.
• Kvadratrottransformasjon: Denne metoden kan også redusere skjevhet, spesielt for positivt skjev data.
• Fjerne uteliggere: Noen ganger kan ekstreme verdier (uteliggere) fjernes eller behandles for å redusere skjevhet.

Å forstå og håndtere skjevhet er viktig for å sikre nøyaktigheten og validiteten av statistiske analyser og tolkninger.