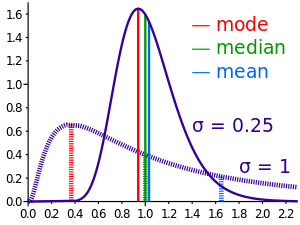
Utvalget/stikkprøvens midtpunkt (Median, gjennomsnitt og modus)

Det finnes flere statistiske metoder som kan benyttes for å angi stikkprøvens midtpunkt og gjennomsnittsverdi. De vanligste er: Median Gjennomsnitt Modus Median Medianen er et sentralitetsmål som angir det midterste tallet/verdien i et ordnet tallsett eller i en stikkprøve (utvalg). Median beregnes ved å dele en stikkprøve eller et utvalg i to like store deler, slik at det er like mange verdielementer på venstre og høyre side. Median er her den midterste verdien. Det vil si den verdien som deler en stikkprøve eller et utvalg i to like store deler. Medianen mål for beliggenhet (midtpunkt) I en stikkprøve på 5 observasjoner, vil X (3) være medianen. For et utvalg der antall observasjoner er et oddetall, er medianen den midterste verdien der utvalget er sortert i rekkefølge. For et utvalg der antall observasjoner er et partall er medianen gjennomsnittet av de to midterste verdiene. Eksempel: La oss se på følgende tall: 1.5% , 2.3% , −3.4% , −5.6% , 0.3% , −3.4% , 3.2% , 2.2% La oss sortere disse i stigende rekkefølge: −5.6% , −3.4% , −3.4% , 0.3% , 1.5% , 2.2% , 2.3% , 3.2% Siden det er n 8 observasjoner, dvs. like antall, så er: Median 0.3% + 1.5% / 2 0,9% Medianen i en stikkprøve symboliseres med tegnet: , og uttales "X -tilda" eller "X krøll". stikkprøvemedian Populasjonsmedianen, dvs. medianen i hele populasjonen, kalles "my tilda" og syboliseres med tegnet: I et sortert datasett med n elementer, hvor n er ulike vil medianen kunne finnes som element nummer . Fordelen ved å bruke median i forhold til gjennomsnitt er at median er stabil overfor ekstreme observasjoner (som blant annet kan fremkomme ved målefeil). Hvis man for eksempel har målt høyder i meter, men har glemt å sette komma i noen av målingene, vil det påvirke gjennomsnittet mye, mens medianen ikke blir påvirket i samme grad. Har man målingene 1,73 – 180 – 1,86, vil gjennomsnittet bli 63,59, mens medianen er 1,86. Her er medianen tett på det som ville vært medianverdien uten den ene feilmålingen (1,80). Videre er median en fordel å benytte ved spørreundersøkelser der en observasjon skiller seg markant fra øvrige observasjoner. Dersom fem personer blir spurt hvor mange husdyr de har, og én av dem bor på gård, kan vi tenke oss dette utfallet: 0, 1, 35, 1, 2. Gjennomsnittet her vil være 7,8 og median 1. Medianen vil her gi en bedre indikasjon på hvor mange husdyr det er vanlig å ha i norske hjem (Wikipedia). Gjennomsnitt Gjennomsnittet, ofte kalt den aritmetiske middelverdien eller bare middelverdien, er summen av alle dataene delt på antall data. Gjennomsnitt er med andre ord en alternativ måte å finne midtpunkt i en stikkprøve eller et utvalg. Gjennomsnittsverdien beregnes ved å summere alle verdiene i stikkprøven og dividere dette tallet med antall undersøkelses enheter. Eksempel Hva er gjennomsnittshøyden for de 30 rekruttene i et tenkt eksemplet? Vi starter med å summerer alle de 30 høydene (verdiene) til studentene og får: 177+181+172+185+...+1895397 Vi har altså 5 397 centimeter å fordele på 30 rekrutter. Gjennomsnittet blir: 5397/30179,9 Gjennomsnittshøyden på rekruttene er altså 179,9 cm, som vi kan runde av til 180 cm. Denne utregningen av gjennomsnittet kan uttrykkes gjennom følgende ligning: Her er de ulike verdiene i populasjonen. Normalt har man bare tilgang til et representativt (tilfeldig) utvalg av en populasjon, og kan bare finne en tilnærmet verdi av gjennomsnittet. Dette symboliseres med μ eller E(X) er en alternativ måte å finne midtpunkt i en stikkprøve eller et utvalg. Gjennomsnittsverdien beregnes ved å summere alle verdiene i stikkprøven og dividere dette tallet med antall undersøkelses enheter. Tegnforklaring: Gjennomsnitt Summer x verdiene n antall undersøkelseenheter. Siden både gjennomsnittsverdien og medianen er mål som skal angi midtpunktet i en stikkprøve er det nærliggende å sammenligne disse to verdiene for å se om det er samsvar mellom dem. Medianen er som tidligere nevnt den midterste verdien i en ordnet stikkprøve, rangert fra laveste til høyeste verdi. For kurs 1 er medianen lik (42+38/2) 40 studenter, mens gjennomsnittet var 35 studenter. Altså en forskjell på 5 studenter. Hva skyldes så forskjellen ? Jo, forklaringen ligger i at medianen ikke er så følsom for ekstremverdier som gjennomsnittet. Det finnes ingen absolutte regler som sier at man skal bruke den ene metoden fremfor den andre. Begge beregningsmetodene er vanlige. Hver imidlertid bare bevist at de kan gi store forskjeller. Mange misbruker denne muligheten til å fremstille en variabel bedre eller dårligere enn den egentlig er, alt ettersom hva som ganger oppdragsgiveren. Men det finnes en tommelfingerregel som jeg anbefaler: Bruk kun gjennomsnitt i stikkprøver som bygger på en normalfordeling. Foreligger det ikke en normalfordeling, bør man bruke median som mål for stikkprøvens midtpunkt. Modus (typetall) Et annet mål for sentraltendens er modus, også kalt typetall. Modus (typetall) er: verdien som forekommer oftest. Dersom flere data forekommer flest antall ganger (For eksempel på en prøve med tallkarakterer der 10 stykker får 5 og 10 stykker får 4), er typetallet gjennomsnittet av disse dataene, eller vi kan operere med flere typetall for datasettet. Eksempel 1 Typetallet behøver ikke å være et tall. I eksemplet med eksamenskarakterer er typetallet karakteren C, siden den karakteren forekommer flest ganger. Eksempel 2 Høyde (cm) Frekvens 170 1 171 1 172 2 173 2 174 1 176 1 177 2 179 2 180 3 181 3 182 5 184 1 185 1 187 1 188 1 189 3 Hva er typetallet i eksemplet med rekrutthøyder? Den høyden som forekommer flest ganger er 182 cm, hele 5 ganger. Derfor er typetallet 182 cm. Forholdet mellom median, snitt og typetall Selv om både median, gjennomsnitt og mode prøver å angi midtpunktet i en stikkprøve (utvalg), vil disse tre beregningene av midtpunktet gi tre forskjllige svar. Noe som er illustrert både i illustrasjonen i toppen av denne siden og illustrasjonen under. Ser vi på illustrasjonen under er ingen av disse tre beregningene av midtpunktet sammenfallene, bortsett fra en symmetrisk fordelig (figur a).

Cookie	Duration	Description
nsid	session	This cookie is set by the provider PayPal to enable the PayPal payment service in the website.
tsrce	3 days	PayPal sets this cookie to enable the PayPal payment service in the website.
x-pp-s	session	PayPal sets this cookie to process payments on the site.

Cookie	Duration	Description
d	3 months	Quantserve sets this cookie to anonymously track information on how visitors use the website.
l7_az	30 minutes	This cookie is necessary for the PayPal login-function on the website.
swpm_session	session	This cookie is set by the Simple WordPress Membership Plugin. This cookie is used for membership login session and to provide access to the protected content on the website.This cookie keeps the login records so user don't want to authorise each time while moving to next page.
_gat	1 minute	This cookie is installed by Google Universal Analytics to restrain request rate and thus limit the collection of data on high traffic sites.

Cookie	Duration	Description
_ga	2 years	The _ga cookie, installed by Google Analytics, calculates visitor, session and campaign data and also keeps track of site usage for the site's analytics report. The cookie stores information anonymously and assigns a randomly generated number to recognize unique visitors.
_gid	1 day	Installed by Google Analytics, _gid cookie stores information on how visitors use a website, while also creating an analytics report of the website's performance. Some of the data that are collected include the number of visitors, their source, and the pages they visit anonymously.
__gads	1 year 24 days	The __gads cookie, set by Google, is stored under DoubleClick domain and tracks the number of times users see an advert, measures the success of the campaign and calculates its revenue. This cookie can only be read from the domain they are set on and will not track any data while browsing through other sites.

Cookie	Duration	Description
anj	3 months	AppNexus sets the anj cookie that contains data stating whether a cookie ID is synced with partners.
c	20 years	This cookie is set by Rubicon Project to control synchronization of user identification and exchange of user data between various ad services.
CMID	1 year	Casale Media sets this cookie to collect information on user behavior, for targeted advertising.
CMPRO	3 months	CMPRO cookie is set by CasaleMedia for anonymous user tracking, and for targeted advertising.
CMPS	3 months	CMPS cookie is set by CasaleMedia for anonymous user tracking based on user's website visits, for displaying targeted ads.
IDE	1 year 24 days	Google DoubleClick IDE cookies are used to store information about how the user uses the website to present them with relevant ads and according to the user profile.
mc	1 year 1 month	Quantserve sets the mc cookie to anonymously track user behaviour on the website.
test_cookie	15 minutes	The test_cookie is set by doubleclick.net and is used to determine if the user's browser supports cookies.
uuid	3 months	MediaMath sets this cookie to avoid the same ads from being shown repeatedly and for relevant advertising.
uuid2	3 months	The uuid2 cookie is set by AppNexus and records information that helps in differentiating between devices and browsers. This information is used to pick out ads delivered by the platform and assess the ad performance and its attribute payment.

Cookie	Duration	Description
CMTS	3 months	No description
cocat1	session	No description
cscat1	session	No description
KHcl0EuY7AKSMgfvHl7J5E7hPtK	20 years	No description available.
LANG	9 hours	No description
sc_f	5 years	No description available.

Utvalget/stikkprøvens midtpunkt (Median, gjennomsnitt og modus)

Median

Kjetil Sander

Lignende artikler

Fordelingsanalyse og frekvensfordeling

Prosentil og kvartil

Variasjonsbredde i utvalget (stikkprøven)

Standardavvik og varians

Univariat analyse og deskriptiv statistikk

Skjevhet og normalfordeling