Hva er standardavvik?
Standardavvik er et mål på verdiens avvik fra gjennomsnittet. Standardavviket viser hvor mye en serie med verdier avviker fra seriens gjennomsnitt.
Standardavviket sier med andre ord noe om hvor stor spredning (variasjon) det er i datamaterialet (utvalget) eller verdiene i et datasett eller av verdien av en stokastisk variabel.
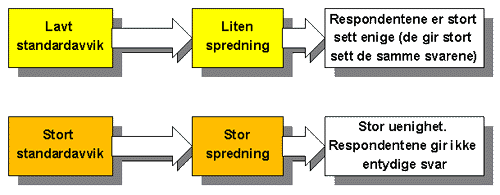
Standardavviket gir verdienes gjennomsnittlige avstand fra gjennomsnittet. Den er definert som kvadratroten av variansen.
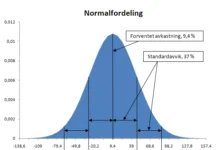
En av grunnene til at standardavviket er en viktig parameter, er Tsjebysjevs ulikhet som sier at de fleste verdiene i et datasett av tilfeldige variabler vil ligge i nærheten av gjennomsnittet, hvor «i nærheten» er definert ved hjelp av standardavviket. Standardavviket ligger på det punktet hvor kurven i normalfordelingen endrer retning.
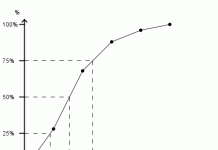
Før man bruker standardavvik bør man bruke et histogram eller en frekvenstabell for å undersøke om datasettet er normalfordelt da mange statistiske metoder ikke kan stoles på om datasettet har skjevhet eller ekstremverdier.