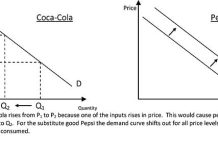
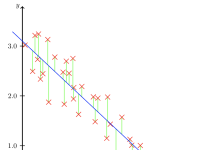
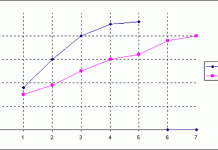
Korrelasjon og kovarians er to statistisk styrkemål vi kan bruke for å finne ut om det er en lineær samvariasjon mellom to variabler. F.eks. om det er en sammenheng mellom markedsføringsinnsatsen og fortjeneste eller omsetning.
Kovarians er:
et styrkemål for den lineære avhengigheten mellom to variabler.
Kovariansen mellom to stokastiske variabler måler hvor mye to variabler varierer sammen (til forskjell fra varians, som måler hvor mye en enkelt variabel varierer i seg selv).
Vi skiller mellom to typer kovarians: Teoretisk- og empirisk kovarians.
Teoretisk kovarians
Teoretisk kovarians er et mål på den underliggende lineære avhengigheten mellom to stokastiske variabler. Kovariansen mellom X og Y noteres ofte som 
. For to stokastiske variabler X og Y er kovariansen definert som:
![{\displaystyle \operatorname {Cov} [X,Y]=E[(X-E[X])(Y-E[Y])]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/69676428f6bd410959617b4a65d219a48bb6876b)
der ![E[\cdot ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/57d488a22bc9f41e976d3afb6036190bcbb36b2e)
er forventning.
Empirisk kovarians
Empirisk kovarians er et estimat av teoretisk kovarians. En estimator for den empiriske kovariansen er:
![{\displaystyle {\widehat {\operatorname {Cov} }}[X,Y]={\frac {1}{n-1}}\sum _{i=1}^{n}(x_{i}-{\bar {x}}_{n})(y_{i}-{\bar {y}}_{n})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc5240414cacd388637e5ad71295aa9f9165ce0a)
der 
er gjennomsnittet av,
og 
er gjennomsnittet av 
.
Kovariansen er skalaavhengig. D.v.s. avhengig av måleskalaen, slik at om skalaen endres vil kovariansen også endres. Derfor er korrelasjon, som ikke er avhengig av skala, et godt alternativ til å måle lineær avhengighet.
For vilkårlige konstanter 
og 
og stokastiske variabler X og Y gjelder
