Lesetid (240 ord/min): 8 minutter

Innholdsfortegnelse
Hva er en kjikvadrattest?
Pearsons kjikvadrattest (Chi-kvadrat test) er en statistisk test for kategoriske data. Det vil si en test for variabler på nominell eller ordinal nivå. Kjikvadrattesten angis ofte som Χ 2, og brukes til å finne ut om dataene dine er vesentlig forskjellig fra det du forventet. Det vil si om det er en signifikant forskjell mellom to kategoriske variabler i en krysstabell. Testen er spesielt nyttig når man ønsker å sammenligne observerte frekvenser med forventede frekvenser i data som er delt inn i kategorier.
To typer kjikvadrattest
Det finnes to typer av Pearsons kjikvadrattest:
Kjikvadrat goodness of fit test
Kjikvadrat goodness of fit test brukes til å teste om frekvensfordelingen til en kategorisk variabel er forskjellig fra dine forventninger. Den lar deg teste om frekvensfordelingen til den kategoriske variabelen er vesentlig forskjellig fra dine forventninger. Ofte, men ikke alltid, er forventningen at kategoriene skal ha like proporsjoner. Brukes for å avgjøre om en enkelt variabel følger en bestemt fordeling.
Eksempel: Undersøke om fordelingen av farger i en pose med M&M’s samsvarer med en forventet fordeling.
Kjikvadrat for uavhengighet
Kjikvadrattest for uavhengighet brukes til å teste om to kategoriske variabler er relatert til hverandre. Testen lar deg teste om de to variablene er relatert til hverandre. Hvis to variabler er uavhengige (urelaterte), påvirkes ikke sannsynligheten for å tilhøre en bestemt gruppe av en variabel av den andre variabelen. Metoden brukes til å avgjøre om fordelingen av én variabel er uavhengig av fordelingen av en annen variabel.
Eksempel: Undersøke om det er en sammenheng mellom kjønn (mann/kvinne) og røykevaner (røyker/ikke-røyker).
Hva skiller disse to kjikvadrattestene?
Hva som skiller dissse to kjikvadrattestene og når du skal bruke dem er sammenfattet i tabellen under.
Kjivadrat Goodness of Fit Test | Kjikvadrattest av uavhengighet | |
| Antall variabler | En | To |
| Formålet med testen | Bestem om en variabel sannsynligvis kommer fra en gitt fordeling eller ikke | Bestem om to variabler kan være relatert eller ikke |
| Eksempel | Bestem om poser med godteri har samme antall stykker av hver smak eller ikke | Bestem om filmgjengernes beslutning om å kjøpe snacks er relatert til typen film de planlegger å se |
| Hypoteser i eksempel | H o : andelen av smaker av godteri er de samme H a : proporsjoner av smaker er ikke de samme | H o : Andelen personer som kjøper snacks er uavhengig av filmtypen H a : andelen mennesker som kjøper snacks er forskjellig for ulike typer filmer |
| Teoretisk fordeling brukt i test | Chi-Square | Chi-Square |
| Grader av frihet | Antall kategorier minus 1
| Antall kategorier for første variabel minus 1, multiplisert med antall kategorier for andre variabel minus 1
|
Kilde: https://www.jmp.com/en_ch/statistics-knowledge-portal/chi-square-test.html
Når bruker vi en kjikvadrattest?
En kjikvadrattest for sannsynlighet brukes når:
- Vi vil teste om en oppgitt sannsynlighetsfordeling stemmer.
- Vi har gjennomført samme undersøkelse to ganger og vil teste om de nye svarene avviker signifikant fra svarende i den første undersøkelsen.
Pearsons kjikvadrattest (Χ 2) er en av de vanligste ikke-parametriske testene. Ikke-parametriske tester brukes for data som ikke følger antakelsene til parametriske tester, spesielt antakelsen om normalfordeling. Testen må brukes hvis vi ønske å teste en hypotese om fordelingen av en kategorisk variabel.
Forutsetninger for å kunne bruke en kjikvadrattest
For å kunne bruke en Pearsons kjikvadrattest må følgende forhold for dataene dine være sanne:
- Du ønsker å teste en hypotese om en eller flere kategoriske variabler. Hvis en eller flere av variablene dine er kvantitative, bør du bruke en annen statistisk test. Alternativt kan du konvertere den kvantitative variabelen til en kategorisk variabel ved å dele observasjonene i intervaller.
- Utvalget ble tilfeldig valgt fra populasjonen.
- Det forventes minimum fem observasjoner i hver gruppe eller kombinasjon av grupper.
- Dataene følger ikke en normalfordeling.
Hvordan utføre en kjikvadrattest?
Kjikvadrattesten er en hypotesetest, hvor vi benytter følgende fremgangsmåten, enten vi benytter en Chi-square goodness of fit-test eller en kjikvadrattest for uavhengighet:
- Definer Nullhypotese (H0) og Alternativ hypotese (H1) før du samler inn dataene.
- Bestem deg for alfaverdien (signifikantnivå). Dette innebærer å bestemme risikoen du er villig til å ta for å trekke feil konklusjon. Anta f.eks. at vi setter α=0,05 når vi tester for uavhengighet. Her har vi bestemt oss for 5 % risiko for å konkludere med at de to variablene er uavhengige når de i realiteten ikke er det. Vi bruker her P-verdien som kriterium for når H0 skal forkastes. Er P-verdien mindre enn signifikantnivået forkaster vi H0 hypotesen. Det vil si hvis P-verdien < 0,05 i dette tilfellet.
- Innhent dataene.
- Sjekk dataene for feil.
- Sjekk forutsetningene for testen.
- Beregn kjikvadratverdien fra dine observerte og forventede frekvenser ved å bruke kjikvadratformelen.
- Finn den kritiske kji-kvadratverdien i en tabell med kritiske kj-kvadratverdier eller bruk statistisk programvare.
- Sammenlign kjikvadratverdien med den kritiske verdien for å finne ut hvilken som er størst.
- Bestem om du vil forkaste nullhypotesen. Du bør forkaste nullhypotesen hvis kjikvadratverdien er større enn den kritiske verdien. Hvis du avviser nullhypotesen, kan du konkludere med at dataene dine er vesentlig forskjellig fra det du forventet.
Begge kjikvadrattestene innebærer å beregne en teststatistikk. Den grunnleggende ideen bak testene er at du sammenligner de faktiske dataverdiene med det som kan forventes dersom nullhypotesen er sann. Teststatistikken innebærer å finne den kvadratiske forskjellen mellom faktiske og forventede dataverdier, og dele denne forskjellen med de forventede dataverdiene. Du gjør dette for hvert datapunkt og legger sammen verdiene.
Deretter sammenligner du teststatistikken med en teoretisk verdi fra chi-kvadratfordelingen . Den teoretiske verdien avhenger av både alfaverdien og frihetsgradene for dataene dine.
Kjikvadratformelen
Begge Pearsons kjikvadrattestene bruker samme formel for å beregne teststatistikken, kjikvadrat (Χ 2 ):
![]()
Hvor:
- Χ 2 er kjikvadratteststatistikken
- Σ er summeringsoperatoren (det betyr “ta summen av”)
- O er den observerte frekvensen
- E er forventet frekvens
Jo større forskjellen er mellom observasjonene og forventningene ( O − E i ligningen), desto større blir kjikvadraten. For å avgjøre om forskjellen er stor nok til å være statistisk signifikant, sammenligner vi kjikvadratverdien med en kritisk verdi.
Kjikvadratfordelingstabellen
Kjikvadratfordelingstabellen (Χ 2 ) er en referansetabell som viser kritiske verdier for kjikvadrat. En kjikvadrat kritisk verdi er en terskel for statistisk signifikans for visse hypotesetester og definerer konfidensintervaller for visse parametere.
Kritiske verdier for kjikvadrat beregnes fra kjikvadratfordelinger. De er vanskelige å beregne for hånd, og det er derfor de fleste bruker en referansetabell eller statistisk programvare i stedet.
Du trenger en kjikvadratkritisk verdi hvis vi ønsker å:
- Beregn et konfidensintervall for en populasjonsavvik eller standardavvik
- Test om variansen eller standardavviket til en populasjon er lik en viss verdi (test av en enkelt varians)
- Test om frekvensfordelingen til en kategorisk variabel er forskjellig fra dine forventninger (chi-square goodness of fit test)
- Test om to kategoriske variabler er relatert til hverandre (kikvadrattest av uavhengighet)
- Test om proporsjonene til to nært beslektede variabler er like (McNemars test)
Kjikvadratfordelingstabell (høyre-hale-sannsynligheter)
Bruk tabellen nedenfor for å finne den kritiske verdien for kjikvadrattesten eller konfidensintervallet. Tabellen gir høyre-hale-sannsynlighetene. Hvis du trenger venstre-hale-sannsynlighetene, må du gjøre en liten tilleggsberegning.
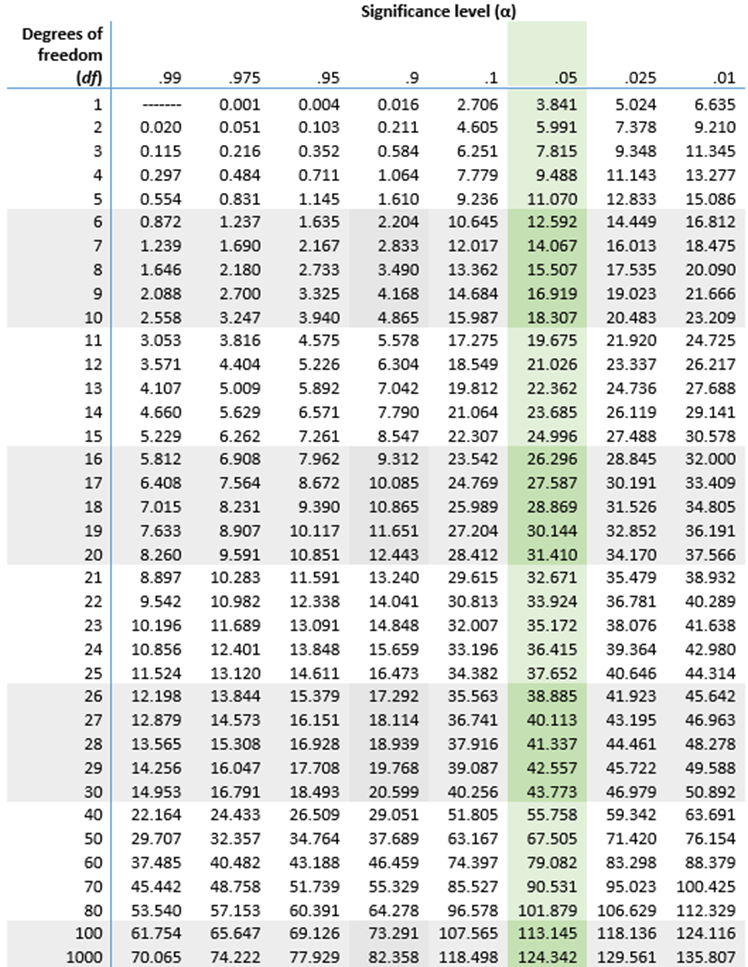
Trinn 1: Beregn frihetsgradene
Det er ikke bare én kjikvadratfordeling – det er mange, og formene deres varierer avhengig av en parameter kalt “frihetsgrader” (også referert til som df eller k ). Hver rad i kjikvadratfordelingstabellen representerer en kjikvadratfordeling med en annen df.
Du må bruke distribusjonen med riktig df for testen eller konfidensintervallet ditt. Tabellen nedenfor gir ligninger for å beregne df for flere vanlige prosedyrer:
| Test eller prosedyre | Frihetsgrader ( df ) ligning |
|---|---|
Test av en enkelt varians Konfidensintervall for varians eller standardavvik | df = prøvestørrelse − 1 |
| Chi-square godhet av passform test | df = antall grupper − 1 |
| Chi-kvadrat test av uavhengighet | df = (antall variabel 1 grupper − 1) * (antall variabel 2 grupper − 1) |
| McNemars test | df = 1 |
Trinn 2: Velg et signifikansnivå
Kolonnene i kjikvadratfordelingstabellen indikerer signifikansnivået til den kritiske verdien. Etter konvensjon er signifikansnivået (α) nesten alltid .05, så kolonnen for .05 er uthevet i tabellen.
I sjeldne situasjoner kan det være lurt å øke α for å redusere Type II-feilfrekvensen eller redusere α for å redusere Type I-feilfrekvensen.
For å beregne et konfidensintervall, velg signifikansnivået basert på ønsket konfidensnivå:
α = 1 − konfidensnivå
Det vanligste konfidensnivået er 95 % (.95), som tilsvarer α = .05.
Trinn 3: Finn den kritiske verdien i tabellen
Du har nå de to tallene du trenger for å finne din kritiske verdi i kjikvadratfordelingstabellen:
- Frihetsgradene ( df ) er oppført langs venstre side av tabellen. Finn tabellraden som tilsvarer frihetsgradene du har beregnet.
- Signifikansnivåene (α) er oppført øverst i tabellen. Finn kolonnen som tilsvarer ditt valgte signifikansnivå.
- Tabellcellen der raden og kolonnen møtes er den kritiske verdien.
Hvordan rapportere en kjikvadrattest
Hvis du inkludere en Pearsons kjikvadrattest i en forsknngsoppgave bør du angi dette i resultatdelen. Følg disse retningslinjene:
- Du trenger ikke oppgi en referanse eller formel siden kjikvadrattesten er vanlig statistikk.
- Referer til kjikvadrat ved å bruke dets greske symbol, Χ 2. Selv om symbolet ligner veldig på en “X” fra det latinske alfabetet, er det faktisk et annet symbol. Greske symboler skal ikke være kursiv.
- Ta med et mellomrom på hver side av likhetstegnet.
- Hvis kjikvadratet er mindre enn null, bør du inkludere en innledende null (en null før desimaltegnet) siden kjikvadratet kan være større enn null.
- Oppgi to signifikante sifre etter desimaltegn.
- Rapporter chi-kvadraten sammen med frihetsgrader , prøvestørrelse og p- verdi, ved å følge dette formatet: Χ 2 (frihetsgrader, N = prøvestørrelse) = kjikvadratverdi, p = p- verdi).
Fordeler med kjikvadrattest
De største fordlene med en kjikvadrattest er:
- Ingen krav til normalfordeling: Kjikvadrattestn er en ikke-parametrisk test, som betyr at den ikke krever at dataene er normalfordelte.
- Fleksibilitet: Kan brukes til å teste uavhengighet mellom to kategoriske variabler eller til å teste om en enkelt variabel følger en bestemt fordeling.
Begrensninger med kjikvadrattest
De største begrensningene med en kjikvadrattest er:
- Antall observasjoner: Testen krever et tilstrekkelig antall observasjoner i hver celle av krysstabellen (vanligvis minst 5) for å gi pålitelige resultater.
- Ikke egnet for små prøver: Hvis prøvestørrelsen er liten, kan chi-kvadrat-testen være upålitelig, og alternative metoder som Fisher’s eksakte test kan være mer passende.
- Skjevhet i frekvenser: Testen er følsom for store skjevheter i frekvensene mellom kategorier, noe som kan påvirke resultatene.
Oppsummering
Kjikvadrattest er et kraftig verktøy for å analysere sammenhenger mellom kategoriske variabler. Den er mye brukt i statistiske analyser innenfor mange felt som samfunnsvitenskap, medisin, markedsføring, og biologi. Selv om den er fleksibel og ikke krever normalfordelte data, er det viktig å være oppmerksom på kravene til prøvestørrelse og forventede frek
Kilder:
- Turney, Shaun – Chi-Square (Χ²) Tests | Types, Formula & Examples (2022). Hentet 03.03.24: https://www.scribbr.com/statistics/chi-square-tests/
- Turney, Shaun – Chi-Square (Χ²) Table | Examples & Downloadable Table (2022). Hentet 03.03.24: https://www.scribbr.com/statistics/chi-square-distribution-table/
- ChatGPT, “Kjikvadrattest”. Hentet 11.08.24: https://chatgpt.com/