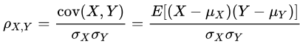Korrelasjon er, i likhet med kovarians, et statisk styrkemål vi kan bruke for å finne ut om det er en lineær samvariasjon mellom to variabler. Er det f.eks. en sammenheng mellom folks høyde og vekt.
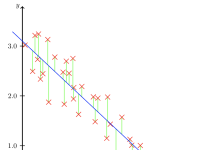
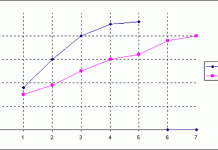
Korrelasjon, eller samvariasjon (skrive vanligvis som cor eller bare r), er et statistisk mål på styrken og retningen mellom to kvantitative variabler. Dvs. hvor mye to målbare størrelser henger sammen med hverandre. F.eks. betyr en positiv korrelasjon mellom inntekt og alder at folk med høy inntekt ofte er eldre enn folk med lav inntekt.
Korrelasjonen angir med andre ord hvilken sammenheng eller rettere sagt statistisk sammenheng som finnes mellom to variabler. Når dette er sagt må det samtidig legges til at korrelasjon mellom to variabler ikke trenger å bety at den ene variabelen er årsak til den andre. Korrelasjon også kan være resultat av spuriøse sammenhenger.
Korrelasjonskoeffisient
Korrelasjon bli ofte målt i en korrelasjonskoeffisient (ofte kun referert til som korrelasjonen). Et er et mål på den underliggende avhengigheten mellom to stokastiske variabler.
Pearsons produkt-moment korrelasjonskoeffisient (eller Pearsons p) er den mest kjente indikatoren på korrelasjon. Den måler samvariasjonen mellom to variabler ved å dele variablenes kovarians på produktet av variablenes respektive standardavvik: