Hva er en faktoranalyse?
Faktoranalyse er ikke en selvstendig analysemetode, men en samlebetegnelse for ulike multivariate analyser som går ut på å analysere avhengighetsforholdet mellom et stort antall variabler, for deretter å forklare deres felles underliggende dimensjoner (faktorer).
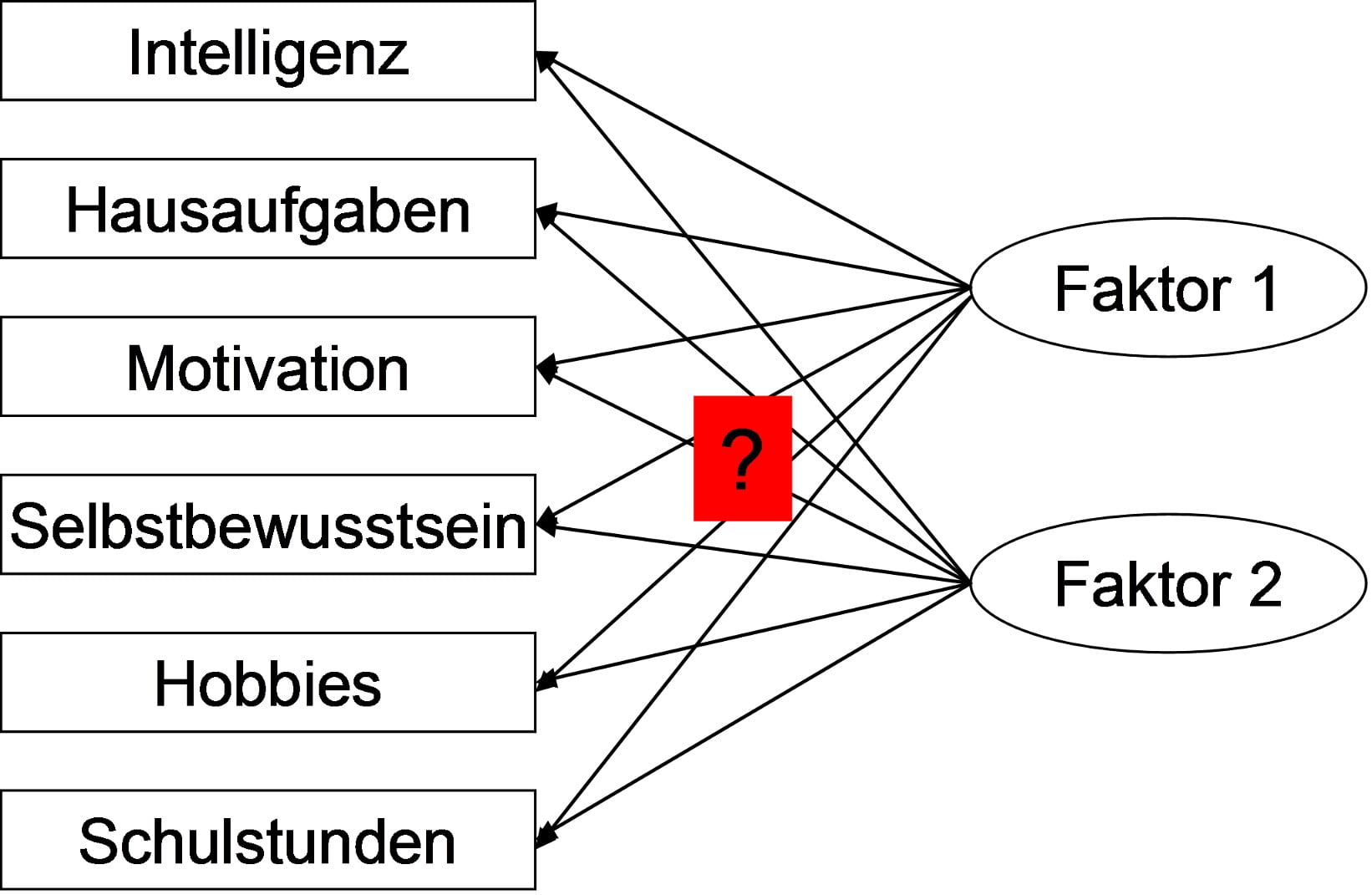
Metoden brukes for å identifisere underliggende strukturer eller faktorer i et stort datasett, gjennom å redusere antall variabler ved å gruppere de som er sterkt korrelert med hverandre, slik at de kan representeres ved færre, underliggende faktorer. Ut i fra f.eks. 50 indikatorer som tar sikte på å forklare en fler-dimensjonal variabel, kan vi gjennom en faktoranalyse redusere dem til noen få. F.eks. til 5 – 6 faktorer. Dette hjelper forskere med å forstå hvilke dimensjoner eller latente variabler som forklarer sammenhengene mellom de observerte variablene.
Faktoranalysen som en matematisk prosedyre søker å forklare mønsteret av samvariasjon mellom observasjoner med utgangspunkt i et minimalt antall grunnleggende dimensjoner. Derfor er faktoranalysen et egnet verktøy for redusere kompleksitet, samt et redskap for å avdekke mulige meningsfulle (tolkbare) og forenklede mønstre i data. Gjennom faktoranalysen forsøker vi å identifisere de grunnleggende dimensjonene eller latente forhold fra klynger (“clusters”) av atferdsformer som er høyt korrelert med hverandre.
Hovedtyper av faktoranalyse
Vi skiller mellom to undergrener av faktoranalysen:
- Eksplorerende faktoranalyse
- Bekreftende faktoranalyse