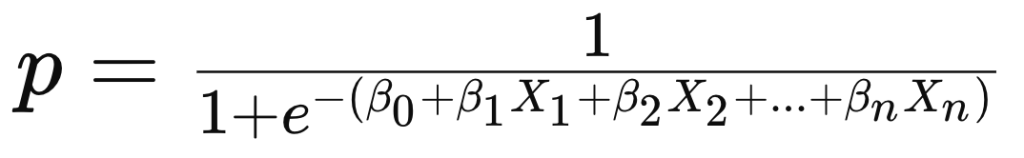Logistisk regresjonsanalyse

Hva er logistisk regresjonsanalyse?

Logistisk regresjonsanalyse er en statistisk metode som brukes til å modellere forholdet mellom en avhengig variabel som er binær (f.eks. ja/nei, suksess/fiasko) og en eller flere uavhengige variabler. Logistisk regresjon brukes når utfallet er dikotomt (to mulige utfall), og målet er å forutsi sannsynligheten for at en hendelse inntreffer basert på de uavhengige variablene. Denne metoden er mye brukt i medisin, samfunnsvitenskap, økonomi, og andre felt hvor forskere ønsker å forstå eller forutsi en binær utfallsvariabel.

Grunnleggende konsepter i logistisk regresjon

Avhengig variabel:

• • Den avhengige variabelen i logistisk regresjon er binær, som betyr at den kun kan ta to verdier, ofte kodet som 0 (ikke-hendelse) og 1 (hendelse).
  • Eksempel: Utfallet av om en pasient har en sykdom (1) eller ikke har sykdommen (0).

Uavhengige variabler:

• • Uavhengige variabler kan være enten kontinuerlige (f.eks. alder, blodtrykk) eller kategoriske (f.eks. kjønn, røykevaner).
  • Eksempel: Alder, blodtrykk, og røyking kan være uavhengige variabler som påvirker sannsynligheten for å ha en sykdom.

Logistisk funksjon (Logit-funksjon):

1. • I stedet for å modellere utfallet direkte, modellerer logistisk regresjon log-odds, som er logaritmen til oddsene for at utfallet er 1.
   • 

2. Sannsynlighetsberegning:

   • Sannsynligheten for at utfallet er 1 (f.eks. at en person har sykdommen) kan beregnes ved å bruke den logistiske funksjonen:
   • Sannsynlighet:
     ​

3. Oddsrater (Odds Ratios):

   • Oddsraten representerer forholdet mellom sannsynligheten for at en hendelse inntreffer og sannsynligheten for at den ikke gjør det. I logistisk regresjon er eksponenten til koeffisienten til en uavhengig variabel tolket som oddsraten.
   • Eksempel: Hvis oddsraten for røyking er 2, betyr det at røykere har dobbelt så høy odds for å ha sykdommen sammenlignet med ikke-røykere.

4. Modelltilpasning og Evaluering:

   • Log-likelihood: En indikator på hvor godt modellen passer dataene. Modeller med høyere log-likelihood passer dataene bedre.
   • Pseudo-R²: En måling som tilsvarer R² i lineær regresjon, men tilpasset logistisk regresjon. Eksempler inkluderer Cox & Snell og Nagelkerke R².
   • Hosmer-Lemeshow-test: En statistisk test som vurderer hvor godt den logistiske regresjonsmodellen passer dataene. En ikke-signifikant p-verdi indikerer en god modelltilpasning.
   • Confusion Matrix: En matrise som viser antall korrekte og feilaktige klassifiseringer gjort av modellen, og brukes til å beregne nøyaktighet, sensitivitet, spesifisitet, og andre målinger.

Eksempel på Logistisk Regresjonsanalyse

La oss si at en forsker ønsker å undersøke hvilke faktorer som påvirker sannsynligheten for at en person har diabetes (binær utfallsvariabel: 1 = har diabetes, 0 = har ikke diabetes). De uavhengige variablene inkluderer alder, kroppsmasseindeks (BMI), og røyking (røyker/ikke-røyker).

Bruksområder for logistisk regresjon

1. Medisinsk forskning:

   • Forutsi sannsynligheten for at en pasient har en sykdom basert på kliniske faktorer som alder, kjønn, symptomer, og laboratorieverdier.
   • Eksempel: Forutsi sannsynligheten for hjerteinfarkt basert på blodtrykk, kolesterolnivå, og familiehistorie.

2. Markedsanalyse:

   • Forutsi sannsynligheten for at en kunde kjøper et produkt basert på demografiske data og kjøpshistorikk.
   • Eksempel: Forutsi sannsynligheten for at en kunde kjøper et bestemt produkt etter å ha mottatt en markedsføringskampanje.

3. Sosial forskning:

   • Forutsi sannsynligheten for at en person stemmer ved et valg basert på alder, utdanning, inntekt, og politiske preferanser.
   • Eksempel: Analysert faktorer som påvirker sannsynligheten for deltakelse i valget.

4. Økonomisk analyse:

   • Forutsi sannsynligheten for at et lån går i mislighold basert på låntakers kredittscore, inntekt, og gjeldsgrad.
   • Eksempel: Forutsi sannsynligheten for mislighold på boliglån.

Fordeler med logistisk regresjon

De største fordlene med logisk regresjon er:

• Fleksibilitet: Kan brukes med både kontinuerlige og kategoriske uavhengige variabler.
• Enkel Tolkning: Oddsrater gjør det relativt enkelt å tolke effekten av uavhengige variabler.
• God Modell for Binære Utfall: Logistisk regresjon er spesielt godt egnet for binære utfall og gir sannsynligheter som alltid ligger mellom 0 og 1.

Begrensninger med logisk regresjon

De største begrensningene med logisk regresjon er:

• Forutsetninger: Modellen forutsetter linearitet i log-odds, fravær av multikollinearitet, og uavhengighet av feilene.
• Dikotom Utfall: Begrenset til binære utfall, selv om utvidelser som multinomisk logistisk regresjon kan håndtere flere kategorier.
• Overfitting: Som med andre modeller, kan logistisk regresjon overtilpasse hvis det er for mange uavhengige variabler i forhold til antall observasjoner.

Logistisk regresjonsanalyse er et kraftig verktøy for å modellere binære utfall og har bred anvendelse i mange forskningsområder. Det gir en fleksibel og tolkbar tilnærming til å forstå hvordan forskjellige faktorer påvirker sannsynligheten for en hendelse.