Kapitalverdimodellen (CAPM)

Kapitalverdimodellen (CAPM) er den mest benyttede teoretiske modellen for å beregne avkastningskravet til et investeringsobjekt, f.eks. en aksje eller bil, sett i forhold til risikoen.

Kapitalverdimodellen sin opprinnelse

Kapitalverdimodellen eller Capital asset pricing model (CAPM) på engelsk, ble utledet av økonomene Treynor (1961/62), Sharpe (1964), Lintner (1965) og Mossin (1966) uavhengig av hverandre på midten av 1960-tallet. Modellen deres er idag er en av de mest sentrale modeller innenfor finans, og bygger videre på arbeidet til Harry Markowitz (1952, 1959) om diversifisering og moderne porteføljeteori . 

I 1990 mottok Sharpe, Markowitz og Merton Miller i fellesskap Nobels minnepris i økonomi for dette bidraget til feltet finansiell økonomi. 

Hva er Kapitalverdimodellen (CAPM)?

Kapitalverdimodellen har i dag  utviklet seg til å bli et verktøy for:

– å estimere den forventede avkastningen sett i relasjon til investeringens risiko. 

Kapitalverdimodellen sitt budskap er at forventet avkastning (avkastningskrav) på et investeringsobjekt bør være summen av en risikofri rente, med et tillegg for en risikopremie som varierer med objektets systematiske risiko (markedsrisiko).

Modellen er en likevektsmodell som gir et avkastningkrav til et aktivum, basert på hvor risikabelt investeringen er i forhold til markedsporteføljen. En modell som gir en teoretisk sammenheng mellom et aktivums forventede avkastning sett i forhold til risikoen over en gitt periode. Modellen forutsetter at aktivumet legges til en allerede vel diversifisert portefølje.

Kapitalverdimodellen (CAPM) sitt formål

CAPM modellens formål er å sørge for at investorene skal få betalt for å ta systematisk risiko. Jo mer slik risiko en investor tar, desto mer avkastning skal investoren få tilbake i forventning.

Formel

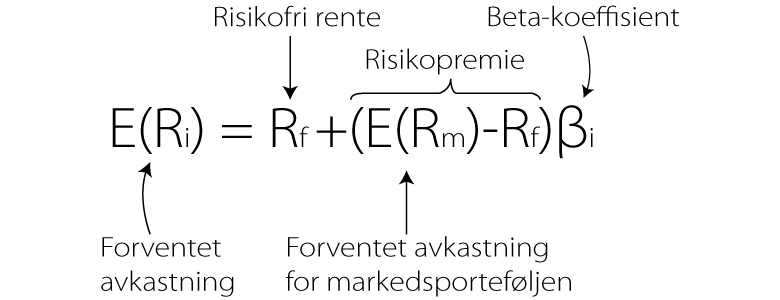
Modellens komponenter kan kort forklares slik:

Risikofri rente er den renten du får uten å ta noen som helst form for risiko. Her bruker vi lang statsobligasjon (typisk 10 år) eller historisk risikofri realrente som referanse.

Beta-koeffisient er markedets systematiske risiko. Altså den risikoen vi ikke kan diversifisert bort. Eksempler på markedsrisiko vi aldri kan diversifisere helt bort er inflasjon, renteøkninger, nedgangstider og markedskollaps.

Risikopremie er meravkastningen du krever ved å påta risiko deg en risiko ved å investere.

Som det går frem av grafen under så øker den forventede avkastning, E(Ri), i takt med den systematiske risikoen, βi. Differansen mellom forventet avkastning for markedsporteføljen og risikofri rente, utgjør risikopremien (Finanssans.no).

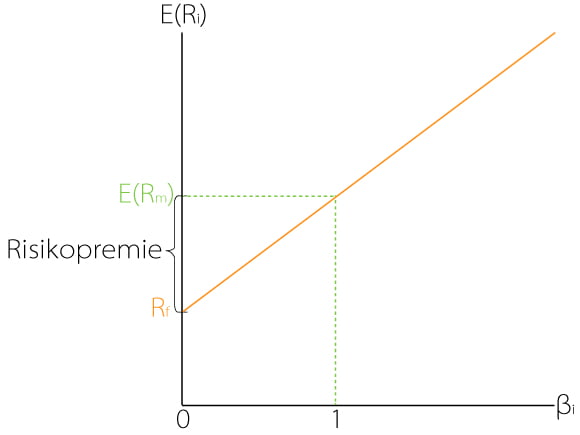
Kapitalverdimodellen (CAPM) er en en-periodisk, framtidig modell som skal beregne et totalkapitalavkastningkrav for tidsperioden mellom t og t+1. 

Kapitalverdimodellens formel er som følger:

Re = Rf + βe x (Rm – Rf)

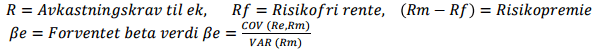
Formelen kan også omskrives slik:

Komponentene i kapitalverdimodellen kan forklares slik:

Avkastningkrav – E(Rj)

Hvilket avkastningkrav [E(Rj)] man beregner kommer her an på hvilken beta (β) som medregnes i modellen. Bruker man for eksempel en aksjebeta beregnes avkastningkravet til egenkapitalen og bruker man totalbeta finner man totalavkastningkravet. Derfor er det viktig å vite hvilken beta man har for å vite hvilket avkastningkrav man til slutt ender opp med. Benyttes totalkapitalmetoden beregner vi en totalkapitalbeta for å beregne totalavkastningkravet. Før vi beregner betaer vil vi starte med å identifisere de to andre komponentene i CAPM-modellen kalt risikofri rente (Rf) og markedets risikopremie [E(Rm)].

Risikofrie renter – Rf

For å beregne det historiske avkastningkravet må vi den finne historiske risikofrie renten. Hvilken risikofrie rente vi bør benytte er avhengig av om hvor langsiktig interesse du har i selskapet eller aksjen. 

For å sette den risikofrie renten anses at det mest korrekte er å bruke den lengste statsobligasjonsrenten (10 år ) og legger til en kalkulert prisstigning (Boye og Koekebakker; 2006). Hvis tidshorisonten for investeringen ikke strekker seg så langt, kan man bruke renten for eksempel for 3-års eller 5-års løpetid.

Har vi et langsiktig perspektiv benytter vi oss av en svært langsiktig rente. For eksempel 10-årig statsobligasjon fra Norges Bank og legge til en kalkulert prisstigning. Har du et kortsiktigere perspektiv benytter vi oss av statsobligasjoner med 3- eller års løpetid. For kortsiktige vurderinger benyttes NIBOR renten som viser den historiske 3 måneders effektive NIBOR renten.

NIBOR renten er:

den renten som brukes når bankene låner seg imellom.

Det antas at denne renten inneholder et risikotillegg på 10 %, og dette trekkes dermed fra for å finne risikofri rente. Deretter justeres denne for kapitalbeskatning etter norske forhold (28 %).

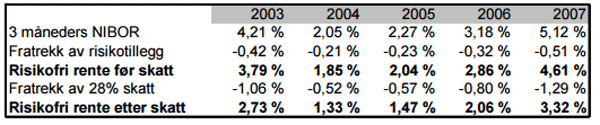
Markedets risikopremie – E(Rm)

Markedets risikopremie (MRP) defineres som:

forskjellen mellom markedsavkastningen og den risikofrie renten

Markedets risikopremie = Forventet avkastning – Risiko avkasting

Markedets risikopremie forteller oss om differansen mellom forventet avkastning på markedsporteføljen og risikofri rente. Størrelsen på markedets risikopremie indikerer hvor stor kompensasjon en investor krever for å investere i markedsporteføljen. Differansen finner man ved å legge til grunn historiske avkastningstall.

Markedets risikopremie [E(Rm)] er den forventede meravkastning ved å ta en høyere investeringsrisiko, enn å holde en risikofri eiendel (Penman 2010). E(Rm) skal reflektere kostnaden per risikoenhet i markedet.

For å finne E(Rm) ser vi på den historiske avkastningen markedet har hatt. Gjennomsnittlig risikopremie på Oslo Børs mellom 1958 og 2005 var på 6,2 % dersom de 10 % høyeste og laveste ses bort fra.Enkelte forhold de siste tjue årene indikerer imidlertid at risikopremien ligger noe lavere nå. Argumentene går ut på at modernisering av børsen, lavere inflasjonsrisiko og mer diversifiserte investorer taler for en risikopremie på 5 % etter skatt.

Markedets risikopremie bygger normalt på historiske tall, og måleperioden varierer vanligvis mellom 10 og vel 100 år. Argumentet for en lang analyseperiode er at man får økt stabilitet og jevner ut store svingninger, argumentet for en kort analyseperiode er at økonomien har vært mye mer stabil de siste 10 år, med for eksempel lavere inflasjon og mer diversifiserte investorer. Det er derfor vanskelig å fastsette en eksakt verdi for markedspremien, markedspremien varierer med valg av analyseperiode (Gjesdal & Johnsen, 1999).

Beta – β

Beta representerer systematisk risiko som er ikke- diversifiserbar, altså risikoen knyttet til egenkapital avkastningen som investor ikke kan bli kvitt ved diversifisering. Betaverdien bestemmes av samvariasjonen mellom avkastning på aksjen og markedets avkastning.

Beta er gitt ved følgende formel:

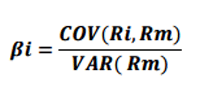
Om selskapet er børsnotert er det greit å finne betaverdien. Dette gjøres da gjennom en regresjonsanalyse av aksjekursen til firmaet og børsindeksen.

Om aksjekursen svinger gjennomsnittlig helt i takt med indeksen har aksjen en betaverdi på 1. Om aksjekursen svinger mer enn markedet (indeksen) vil betaverdien være større enn 1. Videre vil betaverdien være mindre enn 1 dersom aksjekursen svinger mindre enn indeksen (Bøhren og Michalsen 2006).

Beta forteller hvordan et aktivum endrer seg i verdi som følge av svingninger i markedsprisene. Et verdipapir sin beta er:

risikoen verdipapiret bidrar til den optimalt risikable portefølje

Vi kan se på beta-verdien som forholdet mellom gevinst og avkastning. Beta verdien forklarer dermed forskjellene i forventet avkastning. Dette impliserer at investorer vil tilpasse seg langs verdipapirmarkedslinjen. Dette er en grafisk representasjon av forventet avkastning og betaforholdet – risikoen (Bodie, Kane & Marcus, 2011).

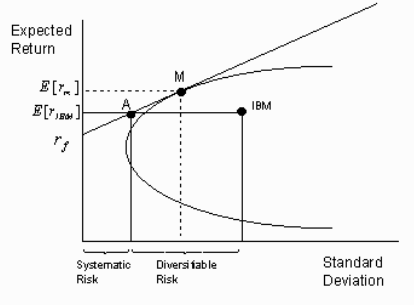
Har et aktivum positiv beta vil dette si at avkastningen på aktivumet beveger seg i samme retningen som avkastningen i markedet generelt.

En negativ beta vil bety at avkastningen på aktivumet beveger seg i motsatt retning av avkastningen i markedet generelt.

Har et aktivum en beta på null vil en endring i markedsavkastningen ikke ha noen betydning på aktivumets avkastning, og det foreligger derfor ingen markedsrisiko og følgelig heller ingen risikopremie. En beta lik 0 tilsvarer med andre ord en risikofri investering, og helningen på verdipapirlinjen tilsvarer aksjemarkedets risikopremie;

Beta representerer selskapets sensitivitet til markedssvingningene. Hvis β=1, vil selskapets forventede avkastning være lik markedets. Har selskapet β<1, vil selskapet svinge mindre enn markedsporteføljen, som betyr at selskapet er utsatt for mindre risiko. Det motsatte gjelder for et selskap med β>1, som derav vil være utsatt for en større risiko (Soffer og Soffer 2002). En aksjebeta gir et mål på hvilken grad aksjen, altså egenkapitalen, er korrelert med markedssvingninger som også er kalt systematisk risiko (Soffer og Soffer 2002). En totalbeta viser risikoen forbundet med hele selskapet uavhengig av finansieringsstruktur og derav inkluderer både egenkapital og gjeld (Soffer og Soffer 2002).

Beta kan finnes på to måter i praksis. Man kan estimere beta på grunnlag av historiske børskurser ved hjelp av regresjonsanalyse av avkastningen til selskapet og markedet. Eller man kan beregne en beta på grunnlag av komparative virksomheter, en såkalt “bottoms-up” beta.

En alternativ metode er å estimere egenkapitalbeta for ikke-børsnoterte virksomheter basert på betaen til komparative virksomheter. I det siste tilfellet bør beta justeres for forskjeller i for eksempel finansieringen av selskapet.

Markedsporteføljen har en beta på 1, mens beta for en risikofri plassering er 0. 

For å estimere beta for et selskap kan vi f.eks. benytte månedlige børsdata for de siste 5-10 årene. Månedlig avkastning kan måles på flere måter, f.eks. kan vi legge til grunn en logaritmisk avkastning for selskapet og Oslo Børs Benchmark Index (OSEBX). Deretter kan vi beregne empirisk kovarians mellom avkastningene, og empirisk varians for avkastningen til OSEBX. Utregningene legger dermed til grunn at relevant systematisk risiko bestemmes av aksjens samvariasjon med det norske markedet.

Meryll Lynch – justering

Dette tallet vil imidlertid også ha ulike former for usikkerhet knyttet til seg som bør korrigeres før vi bruker den beregnede beta-verdien. Her kan vi bruke den såkalte Meryll Lynch – justeringen som går ut på vekte beta-verdien med:

β = 1 med 1/3

Eksempel:
La oss si at vi har kommet frem til en beregnet beta-verdi (β) er på 1,717. For å korrigere denne beta-verdien med Meryll Lynch – justeringen blir regnestykket som følger:

β* = (2/3) * 1,717 + (1/3) * 1,000 = 1,478

Den Meryll Lynch korrigerte beta-verdien blir dermed 1,478 som brukes som gjeldende beta-verdi i kapitalverdi beregningen.

Likviditetspremie

Markedets risikopremie reflekterer investorenes krav til risikokompensasjon for en gjennomsnittlig likvid børsnotert aksje. For ikke-børsnoterte aksjer kan det være aktuelt å justere opp et betabasert egenkapitalkrav med en likviditetspremie. Dahl og Boye (1997) anbefaler likviditetspremier av størrelsesorden 4%-6% for unoterte, og spesielt mindre selskaper som ikke er børsnotert.

Investeringer som er mindre likvide må normalt tilby høyere forventet avkastning for å tiltrekke seg investorer. Likviditetspremien er en kompensasjon for dette. Det er også en risikopremie for at verdien av slike investeringer har en tendens til å falle mye i dårlige tider (Regjeringen 2011-2012). 

Formel for marked i likevekt

Dersom markedet er i likevekt kan den forventede avkastningen til et aktivum beskrives ved hjelp av følgende sammenheng (Bodie, Kane, & Marcus, 2011):

Forklaringen kan også forenklet forklares slik:

Likningen som helhet viser altså at forventet avkastning på et aktivum er lik en kompensasjon for pengenes tidsverdi, uttrykt ved risikofri rente, pluss kompensasjon for å påta seg risiko forbundet med investeringen, også kalt risikopremie og uttrykkes her som beta ganget med markedspremien.

Kapitalverdimodellens forutsetninger

Kapitalverdimodellen bygger på modellen til Harry Markowitz (1952, 1959), om investorers valg av portefølje. I modellen til Markowitz velger en investor en portefølje på tidspunkt t – 1 som gir en stokastisk avkastning på tidspunkt t. Modellen forutsetter videre at investorene er risikoaverse ved valg av portefølje og at de kun er opptatt av gjennomsnittlig avkastning og varians. Som et resultat vil investorene kun holde effisiente porteføljer, det vil si porteføljer som gir den høyeste forventede avkastningen gitt et bestemt nivå av volatilitet eller tilsvarende lavest mulig volatilitet for en gitt forventet avkastning (Fama & French, 2004).

Modellen bygger på følgende forutsetninger (Bodie, Kane & Marcus, 2011):

• Det er mange investorer. Hver med en formue som er liten sammenlignet med den totale formue for alle investorer. Investorer er pristakere (det vil si at prisen er gitt av markedet) og handler som om verdipapirer er upåvirket av deres egne handler, altså perfekt konkurranse.

• Alle investorer planlegger for samme periode. Dette er en myopisk (kort) adferd, ved at den ignorerer alt som kan hende etter denne perioden. Myopisk adferd er generelt suboptimal.

• Investeringer er begrenset til et univers av offentlig omsatte finansielle eiendeler som aksjer, obligasjoner og til risikofrie lån og utlåns muligheter. Det forutsettes at alle investorer kan ta opp eller gi ut lån for alle beløp til en fastsatt risikofri rente.

• Investorer betaler ingen skatt eller transaksjonskostnader på handler eller verdipapirer.

• Alle investorer er ”rational mean optimizers” (i mangel på et bedre norsk ord), noe som betyr at de alle bruker Markowitz’ porteføljeseleksjonsmodell.

• Alle investorer analyserer de risikable aktivaene likt, og deler det samme økonomiske syn på verden. Resultatet er identiske estimater av sannsynlighetsfordelingen av de fremtidige kontantstrømmer fra å identifisere i de tilgjengelige verdipapirer. Dette vil si at investorene har homogene forventninger og trossystem

Svakheter i kapitalverdimodellen

Til tross for at kapitalverdimodellen er den mest utbredte modell for å bestemme avkastningskrav, er forutsetningene mer eller mindre sannsynlige i det virkelige liv. Dette svekker modellens gyldighet (Bodie, Kane & Marcus, 2011).

Kapitalverdimodellen har flere svakheter og begrensninger som kan føre til feil i estimatet av egenkapitalkravet, men den anses likevel som den beste metoden for å gjennomføre slike estimater.

Svakheter ved modellen er bl.a. at parametrene baserer seg i stor grad på investorers forventninger, og disse er både subjektive og variable over tid. Som tidligere nevnt oppstår det i den virkelige verden informasjonsasymmetrier som forhindrer eksistensen av et perfekt kapitalmarked. Denne informasjonsasymmetrien kan føre til at avkastningskravet til aksjen er ulikt innad i selskapet og eksternt hos investorer, og det kan også variere mellom investorer basert på informasjonen de har tilgang til.

Antagelsen om en-periodiske investeringer kan heller ikke forventes å holde for alle investeringer, og det kan derfor være uriktig å bruke avkastningskravet beregnet via kapitalverdimodellen til å diskontere fremtidige prosjekter. Kapitalverdimodellen kan ikke testes, siden man for å kunne teste den trenger å vite den eksakte sammensetningen av den sanne markedsporteføljen og bruke denne i testene. Markedsporteføljen består her ikke bare av verdipapirer, men av alle mulige investeringsobjekter man kunne tenke seg å investere i. Markedsporteføljen blir derfor ikke observerbar.

Forutsetningene som ligger bak kapitalverdimodellen er at vi har et perfekt kapitalmarked, at det ikke eksisterer noen form for transaksjonskostnader eller skatt og at alle investorene har homogene forventninger. Investorer har en-periodisk perspektiv, og inn- og utlånsrente forutsettes å være lik. Modellen kan likevel brukes på tross av disse forutsetningene (Bodie, Kane & Marcus, 2011).

I neste artikkelen oppsummerer vi det vi har gått igjennom i denne artikkelen og ser på hvordan avkastningkravet til egenkapitalen og totalkapitalen beregnes.